Geometric Solution by Bleaug:
Couldn't resist a geometric approach to this one despite the obvious analytical solution...
We are looking for the osculating circle to the parabola in O. This circle is such that for M approaching O, normal in M crosses normal in O (y axis) at osculating circle's center.
Take the [y=x^2] parabola focal point F(0, 0.25). For any point M, the normal crosses the y axis in P such that FP=FM (because all blue angles are equal). Thus, the tangent in M crosses the y axis in Q such that FM=FQ=FP.
When M approaches O, so does Q so FP=FO. So osculating circle to parabola in O is such that OP=0.5 (diameter=1)
Analytic Geometry by Yu (similar submitted by Joe, Bob Ryden and Newzad):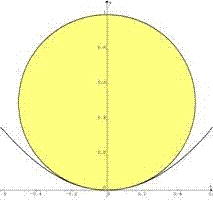
Let r be the radius of the biggest circle that touches the parabola.
x^2 + (y-r)^2 = r^2, y=x^2. Point(s) of contact:
(0,0), ±(√(2r-1), 2r-1).
Same gradient at point(s) of contact: .: dy/dx = -(x/(y-r)) = 2x, i.e., at x=0 or y=r-(1/2).
.: 2r-1=r-(1/2), r=1/2. Hence there is only one point of contact (0,0), and the biggest circle has a diameter of 1.
Do not use all of these Private Money Lender here.They are located in Nigeria, Ghana Turkey, France and Israel.My name is Mrs.Ramirez Cecilia, I am from Philippines. Have you been looking for a loan?Do you need an urgent personal or business loan?contact Fast Legitimate Loan Approval he help me with a loan of $78.000 some days ago after been scammed of $19,000 from a woman claiming to be a loan lender from Nigeria but i thank God today that i got my loan worth $78.000.Feel free to contact the company for a genuine financial call/whats-App Contact Number +918929509036 Email:(fastloanoffer34@gmail.com)
ReplyDelete