Fox 304

Note, the statement should hold in 3-D as well. Don't you agree?

And YES, "plane" is misspelled !

Why?
No, no annoying philosophical stand here.
Just pure simple layyziness.

http://www.8foxes.com/

Fox 302

http://www.8foxes.com/

Fox 300 - Solutions

Bleaug:

Newzad:

Giannno:

http://www.8foxes.com/

Fox 303

Fox Weber: Why are you doing this? What about the human civilization. What happened to the progress they made on internal combustion engine?
Karl Fox: And how about the resources. They were unlimited, right? Those bourgeois deserve worse than this.
Fox Weber: But there are thousands of people making a living on this: honest, hardworking people.
Karl Fox: Oh, you must be talking about the “small people”.
Fox Weber: You’re a pity old man, lost the cause, and now doodling fancy things. See we lost another potential sponsor, thanks to you Karli!
Karl Fox: Don't worry about that. I am working on Chávez as a sponsor. A barrel of oil is still paying pretty good you know.
Fox Weber: Dude, you're hopeless!

http://www.8foxes.com/

Fox 300

We have been delaying this for a while, but Ajit and Vihaan have already solved it. So there is no point of keeping it a secret :)
Note that this may be a general case for Foxes: 296, 297, and 298. It is also related to Fox 301.

It would be great if there are purely geometric solutions!!

http://www.8foxes.com/

Fox 160 - Solutions

Three distinct solutions were found for Fox 160.

The solution commented out by Julian deserves to be presented here. We often had questions inspired from the "things" we observe around us. Julian's solution is the other way. It uses a very casual observation from real-life for the solution. That's perspective lines converge linearly. See the solution below:
by Julian: This one has a simple, intuitive proof. Imagine a long, hollow square-prism. Something like a cardboard tube with a square cross-section. Imagine lines connecting the diagonally-opposite corners of the opposite ends. Due to the symmetry of the tube these four lines will meet at a single point half-way along it.

Now imagine looking through the tube from one end to the other. You see two squares: a large square at the near end, and a smaller square at the far end. By subtly changing the direction the tube is pointing, the far square may move off centre so that the construction looks like the problem diagram. This will not alter the fact that the four lines meet at a single point. QED!

Analytic Geometry by Bob Ryden:

Observe that proving DH implies CG as well (due to rotation). Neat!

Similarity of Triangles by Giannno:

http://www.8foxes.com/

Fox 301

http://www.8foxes.com/

Fox 182 - Solution

Here are two solutions to Fox 182 by Giannno.

Analytic Geometry:

Pythagoras and quadratics:

http://www.8foxes.com/

Fox 299

http://www.8foxes.com/

Fox 298 - Solutions

Solutions to Fox 298.

by Giannno:
by Newzad:

http://www.8foxes.com/

Fox 298

Proving this one immediately solves Foxie 296 and 297.
That's why this is the general case.

http://www.8foxes.com/

Fox 297 - Solutions

by Giannno:

by Bleaug:

Start from an arbitrary AOC triangle such that OC > OA.
Set length unit as (OC-OA)/2 and OA as x.

Reasoning is identical to Fox 296. See its solution.

Polar Fox adds:

By definition OB=x+1 => OBH is an isosceles triangle (1).
Also known that, m(BHO)=90 degrees (2).

Nope, aint gonna happen.

i.e. (1) and (2) can't happen at the same time.

http://www.8foxes.com/

Fox 297

Let's mess around little bit more with this:

http://www.8foxes.com/

Fox 296 - Solutions

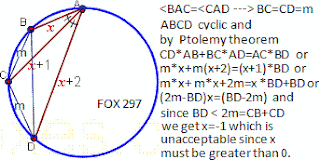
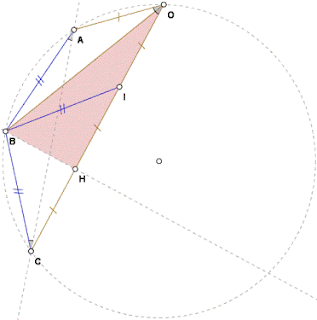Among similar ones, Bleaug finds a contradiction for Fox 296:Take an arbitrary AOC triangle such that OC=3OA. Build B as intersection of triangle's circumscribed circle and AOC internal bisector. B is such that ABC is isoceles, i.e. AB=BC. Symmetry in OABI implies AB=BI, hence IBC is isoceles. Orthogonal projection of B on OC coincides with H such that IH= HC=OA. OHB is rectangle, therefore
OB^2 = (2OA)^2 + BH^2 => OB > 2OA iff angle(AOC) > 0.

Strictly speaking, if angle(AOC)=0 there is a solution if we admit that a straight line is a circle with center at infinity (e.g. in projective plane).

And Giannno solves too:

http://www.8foxes.com/