Fox 267 / Fox 268 - Solutions

Two solutions for Fox 267 and Fox 268:

Bleaug:

Scalar values u=OU and v=OV vary according to a quadratic equation (e.g. apply cosine rule to OUV triangle)
M is a linear function of U and V, hence M coordinates obey some quadratic equation, i.e. M location is a conic. Same applies to N.
Since UV=1, these conics are finite, hence they are ellipses.
Since construction is symmetric, these ellipses are centered in O and have OUV bissectors as symmetry axes.
267: From Fox 266 we know that ON=UN=UV=1, hence N location is a circle of radius 1 centered in O.
268: The skew transform into green ellipse preserves the area. So blue/green ellipse area is twice the red circle area = 2*pi.

Yu: (267)

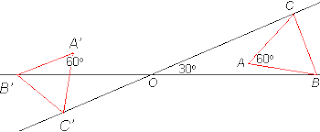
m(BOC) = (½) m(BAC), .: O, B and C are on the circle centred at A, .: OA = AB.
m(B'OC') = (½) m(B'AC'), .: O, B' and C' are on the circle centred at A', .: OA' = A'B'.
AB = A'B', .: OA' = OA. For other orientations refer to Fox 266.
The vertex A is always the same distance from O, so it maps out a circle of radius OA centred at O.

Yu: (268)

The two intersecting lines are y = ±(2 - sqrt(3))x.
Let A(a, (2-sqrt(3))a) and B(b, -(2-sqrt(3))b).
AB^2 = (2-sqrt(3))^2 (a+b)^2 + (a-b)^2 = 1.
By matrix methods, vertex C has x=(sqrt(3)-1)(a+b) and y=-(sqrt(3)-1)(a-b).
.: x^2/(sqrt(3)+1)^2 + y^2/(sqrt(3)-1)^2 = 1, an ellipse.
Area of ellipse = pi (sqrt(3)+1)(sqrt(3)-1) = 2pi