Fox 290

Fox 289

Commonality of the result may imply the existence of a simply solution, which we don't know.
Good luck!

http://www.8foxes.com/

Fox 288

http://www.8foxes.com/

Fox 287

We may have a single solution, but not sure if that's the whole story.

http://www.8foxes.com/

Fox 285 - Solution

Bleaug constructs:
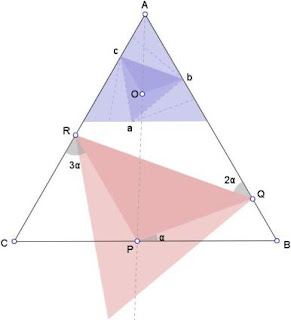
Here is a geometric construction (i.e. compass and ruler) of an inscribed triangle with required property for any angle from 0 to 40°:
1- take any point b on AB and build point c such as angle(Abc)=2α
2- build a inside ABC such as abc is equilateral
3- build O such that angle(Oca)=angle(Oba)=α
4- build P intersection of AO and BC
5- build PQR homothetic to Obc

PQR is such that angle(BPQ)=α, angle (AQR)=2α, angle(CRP)=3α

http://www.8foxes.com/

Fox 286

http://www.8foxes.com/

Fox 285

GEOMETRIC CONSTRUCTION - A Beautiful Greek Antiquity:
(From Weisstein, Eric W. "Geometric Construction." From MathWorld--A Wolfram Web Resource.)
In antiquity, geometric constructions of figures and lengths were restricted to the use of only a straightedge and compass (or in Plato's case, a compass only; a technique now called a Mascheroni construction). Although the term "ruler" is sometimes used instead of "straightedge," the Greek prescription prohibited markings that could be used to make measurements. Furthermore, the "compass" could not even be used to mark off distances by setting it and then "walking" it along, so the compass had to be considered to automatically collapse when not in the process of drawing a circle.

Because of the prominent place Greek geometric constructions held in Euclid's Elements, these constructions are sometimes also known as Euclidean constructions. Such constructions lay at the heart of the geometric problems of antiquity of circle squaring, cube duplication, and angle trisection. The Greeks were unable to solve these problems, but it was not until hundreds of years later that the problems were proved to be actually impossible under the limitations imposed. (Also see Compass and straightedge constructions)

This is our first geometric construction problem, based on a solution submitted by Bleaug. We have a few other construction problems in the queue. For those who are new: the question asks to draw triangle PQR in any equilateral triangle by using a compass, a ruler (without any numbers on it), and angle α (and a piece of paper too :) Let us know if you have any questions!

http://www.8foxes.com/

Fox 284

Another simple one in the series.

http://www.8foxes.com/

Fox 281 - Solution

This solution to 281 was submitted by Bob Ryden. It illustrates Joe's solution as well.

http://www.8foxes.com/

Fox 276 - Solution

Solution to 276 was already known but figure below explains more. By Jim Wilson:

http://www.8foxes.com/

The locus of point P is the arc of a circle. Because the central angle must be twice the subtended arc in measure, the central angle is 60. Thus the major arc has length 10π/6. Since the trajectory would also be over a second arc that is a reflection in AB, the total trajectory is 10π/3.

Fox 283

This one is updated. We received an excellent solution with geometric construction, that will later be our first construction problem. See ya later... http://www.8foxes.com/

Fox 282

http://www.8foxes.com/

Fox 281

http://www.8foxes.com/

Polar fox: Hey Dervish, listen up! You still believe that the life is beautiful, don't you?
Dervish fox: Most definitely!
Polar fox: Here is my problem: the other day, I killed two little polar bunnies. Where is the beauty in that?
Dervish fox: Did you eat them by yourself?
Polar fox: One was for me; the other was devoured by my cubs in the den.
Dervish fox: How did they feel when they were full? Playfully smiling, right?
Polar fox: Oh, I see where you're going...
Dervish fox: Just like that my friend, death of one may be life for another. Seed decays in the darkness of the soil so that flowers bloom in the sun.
Polar fox: I guess I'll need a heart to believe in what you believe.
Dervish fox: I would start with an eye. Don't just look at it, but try to see...

Fox 280

http://www.8foxes.com/