Key words: Geometry, Unusual geometry, Math, Physics, Chemistry, High school, Geometry Olympiads, Free Geometry, Euclidean Geometry, Calculus, Geometric Construction. Oh yes, going-nowhere discussions, haikus, and poems too.
Tuesday, November 30, 2010
Fox 320
Monday, November 29, 2010
Thursday, November 25, 2010
Fox 318
Dervish Fox: I see some beauty between this one and Fox 316.
Red Fox: Would you please help me see that beauty?
Dervish Fox: The term "sin(B)+sin(C)-sin(A)" has evolved into "sin(B+C-A)" in this one. And the rest is identical.
Red Fox: And you found that beautiful?
Dervish Fox: Both answers are very different and very similar at the same time. Don't you feel anything about that?
Red Fox: I am a rational guy. I depend on my intelligence only. I can easily prove both and there is nothing magical or irrational about that. Everything's explainable. Pure and simple!
Dervish Fox: And is that all you can be? Is that the only direction you can grow? Is that who you are, or are you more than that? Why walk when you can fly? Why mutter when you can sing? Why scribble when you can paint?
Red Fox: I think I am starting to feel little bit of annoyance.
Dervish Fox: Not bad for a start my friend, not bad at all !
Wednesday, November 24, 2010
Fox 317
Otherwise, some may consider 12:00:00 as "equally-separated".
Tuesday, November 23, 2010
Wednesday, November 17, 2010
Fox 315
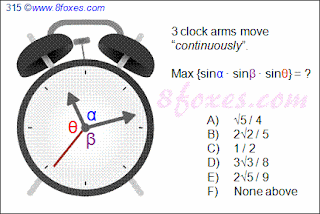
Tuesday, November 16, 2010
Fox 312 - Solutions
Bleaug:
As in Fox 262 (see its solution here) A area (= OQR area below) extremal/constant implies P midpoint of QR. Because:
A constant <=> dA = 0 <=> area(PRR') = area(PQQ') <=> area(P'RR') = area(P'QQ') => PR = PQ when dP tends towards 0.
Hence A = 1 = 2xy or y = 1/2x i.e. answer (D).

Migue:
If area is A the answer is f(x)=y=A/2x.
f(x) is the envelope of all straight lines that close in with axes X-Y constant area equals to A.
Equation of one of this lines is: x/a + y/b = 1 (a,0) in X & (0,b) in Y.
Notice that a & b are two variable parameters.Another equation is: ab/2 = A (area of triangle that straight line draws with axes).
(1) Let f(x,y,a,b)= bx+ay-ab = 0
(2) Let g(a,b)=ab-2A = 0
(3) f'a · g'b - f'b · g'a = 0 (Jacobian of derivatives respect to a and b parameters).
f'a is the derivative of f respect a, ...
y/b - x/a = 0 (3)
If we resolve this system of equations (1),(2) & (3) we obtain:
a = 2x & b = 2y -> ab = 4xy = 2A -> xy = A/2 (equilateral hyperbola)
and y = f(x) = A/2x.
Answer is D) for A =1.








