Key words: Geometry, Unusual geometry, Math, Physics, Chemistry, High school, Geometry Olympiads, Free Geometry, Euclidean Geometry, Calculus, Geometric Construction. Oh yes, going-nowhere discussions, haikus, and poems too.
Saturday, March 26, 2011
Fox 336
Thursday, March 24, 2011
Fox 335
Monday, March 21, 2011
Fox 334
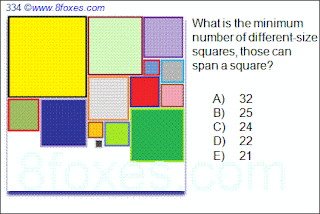 This is more like a google search than a geometry problem, but it is nice to have a reference in our blog as well. Good luck to those who want to try!
This is more like a google search than a geometry problem, but it is nice to have a reference in our blog as well. Good luck to those who want to try!Monday, March 14, 2011
Fox 333

Red Fox: Happy Pi+1 Day!
Himalayan Fox: What is that exactly?
Red: Well, March 14 was the Pi Day, you know, 3.14, and today is March 15th.
Himalayan: But Pi+1 would be 4.14 which is April 14th, isn't it?
Red: Oh, I didn't think that way. Whatever it is, happy March 15th to you brother.
Himalayan: OK, I'll mechanically say "to you too", but can we really happy while thousands of souls swept away with the water?
Red: Well, we can not die with the dead.
Himalayan: But we can help the living.
Red: I hear you brother.
Himalayan: Then we can celebrate 2Pi Day a few months later.
Wednesday, March 9, 2011
Balanced Mancala Problem
We rarely ask pure math problems but here is one with a "very little" touch of geometry. This does not need to be defined as a mancala game, but here it goes:
We have stones coming in batches. Each stone has a color and a weight. If the color of a stone is:
Yellow: It must be placed every other pit (every 2 pits) Batch size is always: 6 Total batches: y Total number = 6y
Red: Must be placed every 3 pits Batch size: 4 Total batches: r Total number = 4r
Green: Must be placed every 4 pits Batch size: 3 Total batches: g Total numbers = 3g
Blue: Must be placed every 6 pits Batch size: 2 Total batches: b Total number = 2b
Purple: Must be placed only once in 12 pits Batch size: 1 Total batches: p Total numbers = p
So there are N=6y+4r+3g+2b+p many stones. The stones in the same batch have the same weight. Different batches may have different weights. WLOG, assume that all weights are integers. We have a proof that ending up with the best well-balanced mancala is very difficult (NP-Hard). Here "well-balanced" means that the pit with the maximum weight is minimized when all stones are distributed. Let's call this maximum pit weight as W.
Consider the following heuristic process:
Step 1. Sort the batches with respect to their weights (batches with the high-weight stones go first) Step 2. Insert the first batch starting from pit number 1. Step 3. Insert the next batch in a way that the total maximum weight throughout 12 pits remains minimum. Step 4. Repeat Step 3 until all batches are placed in the mancala. Let H be the maximum weight throughout 12 pits.
A simple Example: Suppose we have only 4 batches: Yellow (6 stones, each 45 grams) Blue (2 stones, each 40 grams) Yellow (6 stones, each 30 grams) Green (3 stones, each 20 grams) First batch (Yellow) goes to pits: 1, 3, 5, 7, 9, and 11. H=45. Second batch (Blue) goes to pits: 2 and 8. H=45. Third batch (Yellow) goes to pits: 2, 4, 6, 8, 10, and 12. H=70. Fourth batch (Green) goes to pits: 3, 7, and 11. H=70.
In this exercise, heuristic actually finds the optimum, i.e., H=W=70 grams, observed in pits 2 and 8.
And the question: Prove that the worst-case of the heuristic solution, H, is always less than 2W. In other words, W ≤ H ≤ 2W always holds. If you disagree, then try to generate a counter-example.
Good luck!
