Key words: Geometry, Unusual geometry, Math, Physics, Chemistry, High school, Geometry Olympiads, Free Geometry, Euclidean Geometry, Calculus, Geometric Construction. Oh yes, going-nowhere discussions, haikus, and poems too.
Wednesday, March 31, 2010
Fox 270
Monday, March 29, 2010
Fox 266 - Solutions
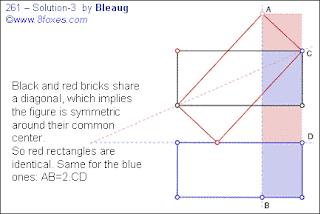
Bleaug:
No words needed. (Hey y not? say somethin' :)
.:B, O and C are on the same circle centred at A. Hence AB = AO.
Giannno:
Friday, March 26, 2010
Wednesday, March 24, 2010
Fox 265 - Solutions
Pure Geometry - Little Trigonometry by Bleaug:
PP'=AA'=2.A'P' therefore tan(angle(PAB))=1/4. Take B' such that PB//P'B' then angle(A'P'B')=angle(PAB). By construction OA'=OB', so tan(a)=A'P'/OA'=2.A'P'/A'B'=2/tan(angle(A'P'B'))=8.
More Trigonometry by Yu:Radius of the small circle is r, radius of the large circle is R.
tanθ = 1/4, tanΦ=tan2θ=2tanθ/(1-tanθ^2) = 8/15
so, r / sqrt(R^2 - r^2) = 8/15 => R = (17/8)r
tan* = r / (R - 2r) = 8.
Let M be the midpoint of LN. Draw OM and ON.
Let radius of small circle = a.
Let PO = x.
Then radius of large circle = 2a + x.
OM = 2a – x.
MN = a.
ON = radius of large circle = 2a + x.
OM^2 + MN^2 = ON^2.
(2a – x)^2 + a^2 = (2a + x)^2
a = 8x
tan (ABC) = tan (POQ) = a/x = 8.
Monday, March 22, 2010
Fox 267
Note that the above is not the only configuration. This one can be classified as "intersection point of the lines can NEVER be in the interior of the equilateral triangle."
Friday, March 19, 2010
Fox 266
Thursday, March 18, 2010
Fox 260 - Solutions
by Bleaug
Let's take as a parabola "well known" property that for any two points U, V of abscissa u, v, the tangent to point T of abscissa (u+v)/2 is parallel to vector UV. (OK! this demonstration would need some cartesian algebra but simple, promise!) From this we derive that for any point M between U and V the area of triangle UMV et less or equal to area of triangle ATV which maximizes triangle height (e.g. assume the opposite and compare area of triangle obtained from M+dM)
Then let's assume U and V achieve the maximum trapezoid area between A (x=0) and B(x=2), then necessarily Au=uv and uv=vB which implies Au=uv=vB=AB/3=2/3. Because of symmetry, maximum area is equivalent to area of rectangle AvVW = 8/9 * 4/3 = 32/27.
Geometric Translation
by Yu
Translate y=2x-x^2 to the left by 1 unit to obtain y=1-x^2.
Without going into details, the area of the trapezium is greater than the area of the quadrilateral. Area of trapezium, A = (1/2) (2x+2)(1-x^2) = (x+1)(1-x^2)
Max A = 32/27 when x = 1/3.
For more details see Fox 260.
http://www.8foxes.com/
Wednesday, March 17, 2010
Fox 265
Red fox: Little changes lead nowhere! What we need is a whole scale revolution.
Polar fox: What are you suggesting? Rewriting Euclid's axioms?
Red fox: Why not? Define a new basis, set up a new geometry and build a new universe.
Polar fox: Dude, you're beyond here. I think you need a change.
Tuesday, March 16, 2010
Sunday, March 14, 2010
Friday, March 12, 2010
Wednesday, March 10, 2010
Fox 262
Tuesday, March 9, 2010
Monday, March 8, 2010
Fox 260
Saturday, March 6, 2010
Fox 12
Friday, March 5, 2010
Fox 255 - Solutions
Heron's Formula by Wilson:
Thursday, March 4, 2010
Fox 259
Wednesday, March 3, 2010
Fox 258
Tuesday, March 2, 2010
Fox 256 Solution
= area of parallelogram ABEF = area of parallelogram ABCD
http://www.8foxes.com/