Fox 279

http://www.8foxes.com/

Fox 262 - Solutions

Two solutions to Fox 262

Bleaug:
OAB is minimal for any M fixed (and making AB slope vary) when M is the midpoint of AB. This is intuitively depicted in the following picture where brown and green triangles have the same area (assuming first degree differentiation approximation) which means that OAB area is extremal. This extremum is a minimum because OAB area is a continuous function and it reaches infinity when A or B reaches infinity.

This means that the point M we are looking for is such that M is midpoint of AB and AB tangent in M. This brings us to problem 260 where we already encountered point V(4/3, 8/9):
- tangent in V is parallel to UP and vector(UP) = vector(VB) because of parabola property (see Fox 260)
- vector(UP) is symmetric of vector(VO) along y axis because of parabola symmetry
- thus OVB is isoceles and V is the midpoint of AB

Thus V achieves minimal OAB area.
Area = 4/3 . 16/9 = 64/27.

By Yu:

Equation of tangent at x=a, y=-(2a-2)x+a^2.
Area of triangle = (a^4)/(4(a-1)).
When a=4/3, minimum area = 64/27.
Question: a=4/3 in Fox 260 and Fox 262. Is this a coincidence?

http://www.8foxes.com/

Fox 278

http://www.8foxes.com/

Fox 277

This is a strong statement that does not depend on the type of ellipse.

Has anybody seen something similar anywhere else?
http://www.8foxes.com/

Fox 276

http://www.8foxes.com/

Fox 272 - Solution

Yu claims the following:
Without the parabolic track a particle (initially at rest) at the vertex will be in free fall and drops at maximum acceleration of g. With the parabolic track the motion is restricted by the track and the particle is no longer in free fall; it slides down the track with increasing speed. Will it leave the track at some point?

All parabolic tracks are similar (See Fox 270). Consider the track y=-x^2 which ends at the point (x,-x^2).

When a particle slides from rest at the vertex (0,0) to the point (x,-x^2), it acquires speed v=sqrt(2gx) in the direction given by tanθ=dy/dx=-2x, where θ is the angle with the x-axis.
.: cosθ = 1/sqrt(1+4x^2), sinθ=-2/sqrt(1+4x^2).

At point (x,-x^2) the particle is in free fall,
v_H=sqrt(2gx)/sqrt(1+4x^2),
v_y=-2sqrt(2gx^2)/sqrt(1+4x^2).

After a further time Δt, Δx=sqrt(2gx)Δt/sqrt(1+4x^2),
Δy=-2sqrt(2gx^2)Δt/sqrt(1+4x^2) - (1/2)g(Δt)^2
= -2xΔx-(1+(1/4x^2))(Δx)^2,
and the particle is at y=-x^2 - 2xΔx -(1+(1/4x^2))(Δx)^2.

If the track did not end at (x,-x^2) but continued to infinity,
y=-(x+Δx)^2
= -x^2-2xΔx-(Δx)^2 > -x^2 - 2xΔx -(1+(1/4x^2))(Δx)^2.
.: The particle stays on the parabolic track.

Fox 275

http://www.8foxes.com/

Fox 274

http://www.8foxes.com/

Fox 271 - Solutions

Two solutions for Fox 271.
Geometric Solution by Bleaug:

Couldn't resist a geometric approach to this one despite the obvious analytical solution...
We are looking for the osculating circle to the parabola in O. This circle is such that for M approaching O, normal in M crosses normal in O (y axis) at osculating circle's center.
Take the [y=x^2] parabola focal point F(0, 0.25). For any point M, the normal crosses the y axis in P such that FP=FM (because all blue angles are equal). Thus, the tangent in M crosses the y axis in Q such that FM=FQ=FP.
When M approaches O, so does Q so FP=FO. So osculating circle to parabola in O is such that OP=0.5 (diameter=1)

Analytic Geometry by Yu (similar submitted by Joe, Bob Ryden and Newzad):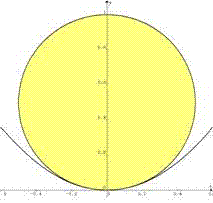
Let r be the radius of the biggest circle that touches the parabola.
x^2 + (y-r)^2 = r^2, y=x^2. Point(s) of contact:
(0,0), ±(√(2r-1), 2r-1).
Same gradient at point(s) of contact: .: dy/dx = -(x/(y-r)) = 2x, i.e., at x=0 or y=r-(1/2).
.: 2r-1=r-(1/2), r=1/2. Hence there is only one point of contact (0,0), and the biggest circle has a diameter of 1.

http://www.8foxes.com/

An Interesting Property of Relatively-Prime Numbers

Hello Guys,
There are a few more parabola questions in line, but I need to solve a number theory question. I have a proof but it is very long and clumsy. I am looking for a slicky solution. Here it goes:

a and b are relatively-prime integers such as,
3 and 8 (e.g. GCD(3,8)=1).
Let N=ab.
Let 1 ≤ k ≤ a, and 1 ≤ m ≤ b, both are integers.
Let set A be all integers, x=k+ia AND x ≤ N AND i=0,1,...
Let set B be all integers, y=m+jb AND y ≤ N AND j=0,1,...

PROVE THAT A∩B contains one integer only.

Example:
a=3, b=8, GCD(3,8)=1
N=24
Let k=2 and m=6.
A={2, 5, 8, 11, 14, 17, 20, 23}
B={6, 14, 22}
A∩B={14}
Note that the above statement is true for any k and m satisfying
1≤k≤a, and 1≤m≤b respectively.

It is very obvious that there should be a short and beautiful proof.

Fox 269 - Solution

By Yu:

0 ≤ α ≤ 60

Large Ellipse

Semi-major axis: (1/2)(√3 + cot(α/2))
Semi-minor axis: (1/2)(√3 - tan(α/2))
Area = π*major*minor=(π/2)(√3 cotα + 1).

Small Ellipse

Semi-major axis: (1/2)(tan(α/2) + √3)
Semi-minor axis: (1/2)(cot(α/2) - √3)
Area = π*major*minor = (π/2)(√3 cotα - 1).

Ratio of their areas (large : small) = (√3 cotα + 1)/(√3 cotα - 1)
= [(√3/2)cosα + (1/2)sinα] / [(√3/2)cosα - (1/2)sinα]

= sin(60+α) / sin(60-α)

60 ≤ α ≤ 90
Large Ellipse: Area = (π/2)(1 + √3 cotα)

Small Ellipse: Area = (π/2)(1 - √3 cotα)

Ratio of their areas (large : small) = (1 + √3 cotα)/(1 - √3 cotα)
= [(1/2)sinα + (√3/2)cosα] / [(1/2)sinα - (√3/2)cosα]

= sin(α+60) / sin(α-60).

An observation:
When α=60, the ratio is undefined because the area of the small ellipse is 0. The third vertex maps out a straight line.

Fox 273

http://www.8foxes.com/

Fox 267 / Fox 268 - Solutions

Two solutions for Fox 267 and Fox 268:

Bleaug:

Scalar values u=OU and v=OV vary according to a quadratic equation (e.g. apply cosine rule to OUV triangle)
M is a linear function of U and V, hence M coordinates obey some quadratic equation, i.e. M location is a conic. Same applies to N.
Since UV=1, these conics are finite, hence they are ellipses.
Since construction is symmetric, these ellipses are centered in O and have OUV bissectors as symmetry axes.
267: From Fox 266 we know that ON=UN=UV=1, hence N location is a circle of radius 1 centered in O.
268: The skew transform into green ellipse preserves the area. So blue/green ellipse area is twice the red circle area = 2*pi.

Yu: (267)

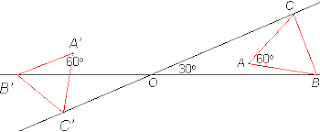
m(BOC) = (½) m(BAC), .: O, B and C are on the circle centred at A, .: OA = AB.
m(B'OC') = (½) m(B'AC'), .: O, B' and C' are on the circle centred at A', .: OA' = A'B'.
AB = A'B', .: OA' = OA. For other orientations refer to Fox 266.
The vertex A is always the same distance from O, so it maps out a circle of radius OA centred at O.

Yu: (268)

The two intersecting lines are y = ±(2 - sqrt(3))x.
Let A(a, (2-sqrt(3))a) and B(b, -(2-sqrt(3))b).
AB^2 = (2-sqrt(3))^2 (a+b)^2 + (a-b)^2 = 1.
By matrix methods, vertex C has x=(sqrt(3)-1)(a+b) and y=-(sqrt(3)-1)(a-b).
.: x^2/(sqrt(3)+1)^2 + y^2/(sqrt(3)-1)^2 = 1, an ellipse.
Area of ellipse = pi (sqrt(3)+1)(sqrt(3)-1) = 2pi

Fox 272

http://www.8foxes.com/

The claim assumes that there is a positive gravity in the given direction.

So, it should hold in Pluto as well.

Himalayan fox: Here is a claim ready to be blown away with a single counterexample. How strong is your theory Polar?
Polar fox: Well, I can smell it.
Himalayan fox: It demands more than that. Are you living in a paper castle ready to be drifted away by the next wind? Or are you a real believer of something that even the strongest quake can not shake you a bit - you stand firmly on the ground?
Polar fox: No problem on my stand man! I am not shaken at all, but... the thing is... the ice is melting!

Fox 271

http://www.8foxes.com/