Happy new year to all, by the way!
Key words: Geometry, Unusual geometry, Math, Physics, Chemistry, High school, Geometry Olympiads, Free Geometry, Euclidean Geometry, Calculus, Geometric Construction. Oh yes, going-nowhere discussions, haikus, and poems too.
Sunday, January 27, 2013
Monday, April 11, 2011
Fox 338

Thursday, April 7, 2011
Fox 337
Tuesday, February 1, 2011
Fox 327
Earth is not a perfect sphere,
It's a geoid of some kind,
Not perfectly-round but close enough.
A year is a little more than 365 days.
A day is not exactly 24 hours,
little short of that.
Pi is more than 3.
Twenty-two over seven is not far off though,
often close enough.
Man hardly lives a 100 years.
Few goes beyond,
Some get close enough.
Truth ascends above digits,
distorts formulas,
bends orbits.
Man searches it with greed,
never reaches,
never conquers.
So my dear,
give up the precision,
stop running the numbers.
Instead,
smell the soil after rain,
hold a cuddling baby in your hand,
wander your vision from Vega to Orion,
let a snowflake die in your palm.
hear what morning breeze tells,
Then round up what you got.
A little more or a little less.
Even if it is still not found,
You're close enough.
--- Polar Fox
Sunday, January 16, 2011
Fox 320 - Solutions
 This fox has been discussed extensively. See here...
This fox has been discussed extensively. See here...1. Calculus by Bleaug
He says: "I spotted this problem in a Paul Halmos book "Problems for mathematicians, young and old, 1991", actually in a French translation. He provided the solution below (reformulated by myself) as being proposed by Hugh Montgomery in 1985 in some Math Conference."

2. Checkerboard Solution by Rochberg and Stein:
- Call sub rectangles as TILEs.
- Start from the lower left corner of the overall rectangle (let's call this point as the origin)Draw horizontal and vertical lines separated by 1/2=0.5 units starting from the origin.
- This will create 0.5 x 0.5 squares (and possibly rectangles around 2 edges -top and/or RHS)
- Color the first square (that has the origin as one of its corners) as black the next one as white, and so on to generate a checkerboard-look.
- Each TILE will have equal areas of black and white (Why?)
- Therefore the overall rectangle will have equal areas of black and white.
- So overall rectangle has at least one integer side.
H means the horizontal side is integer, and V means that the vertical side is integer. a1 is the square at the origin. There could have been a smarter combination, but this simple one illustrates the process clearly. This looks like the closest geometric solution we can get -at this time.
 When there's hardly no day nor hardly no night
When there's hardly no day nor hardly no nightThere's things half in shadow and halfway in light
3. Induction by Robinson
- Assume that each H-tile has a width of 1, and each V-tile has a height of 1. Note that any rectangle can be converted this way without distorting the original problem. (This may increase the number of tiles significantly though)
- Chose any H-tile, say T(0). (If there is no H-tile, then the result is immediate)
- If there are H-tiles whose lower border shares a segment with T(0)'s upper border, choose one and call it T(1).
- Otherwise only V-tiles share this border. In this case, we can expand T(0) upward 1 unit. This does not increase the number of H-tiles. Also, the cut V-tiles still have height 1. (They are still V-tiles)
- Continue expanding T(0) until either the top of the rectangle is reached or a choice of an adjacent H-tile T(1) is possible.
- Then repeat the same process from T(1). (Continue upward similarly from T(1) to get T(2), and so on...)
- This will result in a chain of T(0), T(1), T(2), ... , T(m).
- Starting from T(0) again, work downward similarly to obtain a bigger chain:
T(-n), T(1-n), ... , T(0), T(1), ... , T(m-1), T(m) of H-tiles stretching from bottom to top. - Remove these tiles and slide the rest together to get a rectangle with fewer H-tiles.
- Induction applied to this smaller rectangle yields the result for the original rectangle.
Tuesday, November 30, 2010
Fox 320
Saturday, November 6, 2010
Fox 313
Sunday, June 27, 2010
Fox 295
Friday, June 25, 2010
Fox 293 - Solutions
by Bob Ryden: (Ajit commented a very similar one)

by Bleaug:

Two tangents to a given circle define a symmetric 'kite' figure. By construction, the two kites defined by OUV and OTU are isometric because they have identical short legs. Since angles in T, U, V are right angles, blue and green angles are supplemental. Hence, angle a is angle(OUV). From Thales theorem we get cos(a) = 1/3
by Yu:
Several steps remain implicit in the figure. More words may be needed for a formal proof. But the solution holds.

by Binary Descartes:

Common tangents from the same point have equal lengths.
See the two identical deltoids (kites) sharing the same side.
Then cos(a) = e/3e = 1/3.
http://www.8foxes.com/
Thursday, June 24, 2010
Fox 294
Friday, June 18, 2010
Fox 293
There are about 5 different solutions, that we can post in coming days.
Sunday, March 14, 2010
Fox 261 - Solutions




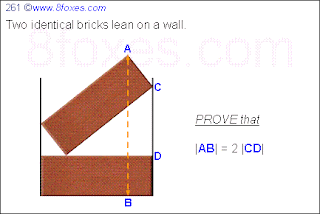
Tuesday, March 9, 2010
Fox 261
Also there are at least 3 purely-geometric solutions...
Saturday, March 6, 2010
Fox 12
 http://www.8foxes.com/
http://www.8foxes.com/Friday, March 5, 2010
Thursday, February 25, 2010
Monday, February 22, 2010
Fox 252
Saturday, February 13, 2010
Fox 243 - Solution
Friday, February 12, 2010
Fox 244
Look into thy heart, and see,
--- Dervish Fox