by Bleaug
Let's take as a parabola "well known" property that for any two points U, V of abscissa u, v, the tangent to point T of abscissa (u+v)/2 is parallel to vector UV. (OK! this demonstration would need some cartesian algebra but simple, promise!) From this we derive that for any point M between U and V the area of triangle UMV et less or equal to area of triangle ATV which maximizes triangle height (e.g. assume the opposite and compare area of triangle obtained from M+dM)

Then let's assume U and V achieve the maximum trapezoid area between A (x=0) and B(x=2), then necessarily Au=uv and uv=vB which implies Au=uv=vB=AB/3=2/3. Because of symmetry, maximum area is equivalent to area of rectangle AvVW = 8/9 * 4/3 = 32/27.
Geometric Translation
by Yu
Translate y=2x-x^2 to the left by 1 unit to obtain y=1-x^2.
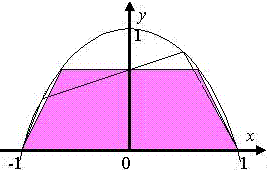
Without going into details, the area of the trapezium is greater than the area of the quadrilateral. Area of trapezium, A = (1/2) (2x+2)(1-x^2) = (x+1)(1-x^2)
Max A = 32/27 when x = 1/3.
For more details see Fox 260.
http://www.8foxes.com/