Here, we received a claim that a solution was found again. It should not be terribly hard. Enjoy...
Key words: Geometry, Unusual geometry, Math, Physics, Chemistry, High school, Geometry Olympiads, Free Geometry, Euclidean Geometry, Calculus, Geometric Construction. Oh yes, going-nowhere discussions, haikus, and poems too.
Tuesday, July 19, 2011
Fox 9
Here, we received a claim that a solution was found again. It should not be terribly hard. Enjoy...
Thursday, February 10, 2011
Fox 15 - Solution
Chrome, Firefox, Opera, Safari, or IE Explorer 9.0.
Sunday, January 9, 2011
Fox 15

Friday, January 7, 2011
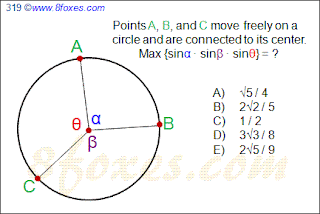
Fox 319 - Solutions

Trigonometry and calculus by Six:
x + y + z = 360 and sinx*siny*sinz
-> f(x,y) = sin(x)*sin(y)*sin(360-x-y)
-> f(x,y) = sin(x)*sin(y)*-sin(x+y)
Now to find the critical points of f(x,y), we just need to find the partial derivative with respect to x and y and solve for 0.
f_x(x,y) =
sin(x)sin(y)(-cos(x+y)-cos(x)sin(y)sin(x+y)
solve for 0.
sin(x)sin(y)(-cos(x+y)-cos(x)sin(y)sin(x+y)=0
-> tan(x) = -tan(x+y)
Since the function is symmetric, we should get the same partial derivative for y.
-> tan(y) = -tan(y+x)
-> tan(x)=tan(y)
-> x = y or they are opposites. However, if they are opposites, the original function just becomes 0. Thus, x = y.
Now substitute in x for y in the original equation and find its critical points.
Eventually, you will get sin(3x)=0
x = 120 degrees
y = 120 degrees
z = 120 degrees
Answer (D)
Sunday, December 19, 2010
Year-End Note
We heard a call from South,
saying, "Come - whoever you are!"
"Poor or rich"
"Full or null"
"Up or down"
"Live or dull"
"Come, just hear my cry!"
It was not the ears heard the call,
But the heart trembled with it.
How can one remain unconscious to this call?
So my friend,
never reject a good call.
Shine with your mercy
upon everyone.
Break your daily routine,
Do things out of the box.
Search the good in bad,
And never give up thinking.
--- Polar Fox
Friday, December 10, 2010
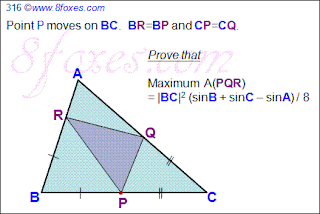
Fox 316 and 318 - Solutions
Fox 316 Solution:
Bleaug:
"I couldn't get a pure geometric demonstration of these two problems. At best, with some lazy observations you are able to show that for both #316 and #318, maximum area is achieved for P midpoint of BC:
a) angle(QPR) in P remains constant when P varies
b) PR/PB is constant
c) PQ/PC is constantHence area(PQR) is proportional to PB.PC which is maximized when P is the midpoint of BC.
The rest is obtained by calculus."

Fox 318 Solution:

Monday, December 6, 2010
Fox 322
Wednesday, December 1, 2010
Monday, November 29, 2010
Thursday, November 25, 2010
Fox 318
Dervish Fox: I see some beauty between this one and Fox 316.
Red Fox: Would you please help me see that beauty?
Dervish Fox: The term "sin(B)+sin(C)-sin(A)" has evolved into "sin(B+C-A)" in this one. And the rest is identical.
Red Fox: And you found that beautiful?
Dervish Fox: Both answers are very different and very similar at the same time. Don't you feel anything about that?
Red Fox: I am a rational guy. I depend on my intelligence only. I can easily prove both and there is nothing magical or irrational about that. Everything's explainable. Pure and simple!
Dervish Fox: And is that all you can be? Is that the only direction you can grow? Is that who you are, or are you more than that? Why walk when you can fly? Why mutter when you can sing? Why scribble when you can paint?
Red Fox: I think I am starting to feel little bit of annoyance.
Dervish Fox: Not bad for a start my friend, not bad at all !
Tuesday, November 23, 2010
Wednesday, November 17, 2010
Fox 315

Thursday, May 20, 2010
Fox 289
Good luck!
Wednesday, April 28, 2010
Fox 262 - Solutions
OAB is minimal for any M fixed (and making AB slope vary) when M is the midpoint of AB. This is intuitively depicted in the following picture where brown and green triangles have the same area (assuming first degree differentiation approximation) which means that OAB area is extremal. This extremum is a minimum because OAB area is a continuous function and it reaches infinity when A or B reaches infinity.
This means that the point M we are looking for is such that M is midpoint of AB and AB tangent in M. This brings us to problem 260 where we already encountered point V(4/3, 8/9):
- tangent in V is parallel to UP and vector(UP) = vector(VB) because of parabola property (see Fox 260)
- vector(UP) is symmetric of vector(VO) along y axis because of parabola symmetry
- thus OVB is isoceles and V is the midpoint of AB
Thus V achieves minimal OAB area.
Area = 4/3 . 16/9 = 64/27.
By Yu:

Area of triangle = (a^4)/(4(a-1)).
When a=4/3, minimum area = 64/27.
Thursday, April 15, 2010
Thursday, March 18, 2010
Fox 260 - Solutions
by Bleaug
Let's take as a parabola "well known" property that for any two points U, V of abscissa u, v, the tangent to point T of abscissa (u+v)/2 is parallel to vector UV. (OK! this demonstration would need some cartesian algebra but simple, promise!) From this we derive that for any point M between U and V the area of triangle UMV et less or equal to area of triangle ATV which maximizes triangle height (e.g. assume the opposite and compare area of triangle obtained from M+dM)

Then let's assume U and V achieve the maximum trapezoid area between A (x=0) and B(x=2), then necessarily Au=uv and uv=vB which implies Au=uv=vB=AB/3=2/3. Because of symmetry, maximum area is equivalent to area of rectangle AvVW = 8/9 * 4/3 = 32/27.
Geometric Translation
by Yu
Translate y=2x-x^2 to the left by 1 unit to obtain y=1-x^2.
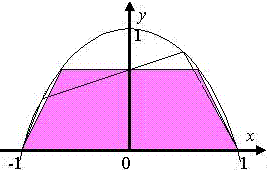
Without going into details, the area of the trapezium is greater than the area of the quadrilateral. Area of trapezium, A = (1/2) (2x+2)(1-x^2) = (x+1)(1-x^2)
Max A = 32/27 when x = 1/3.
For more details see Fox 260.
http://www.8foxes.com/
Wednesday, March 10, 2010
Fox 262
Monday, March 8, 2010
Fox 260
Saturday, March 6, 2010
Fox 12
 http://www.8foxes.com/
http://www.8foxes.com/