This is just one step forward to the general case. Should not be very hard unless the claim is wrong :)
Key words: Geometry, Unusual geometry, Math, Physics, Chemistry, High school, Geometry Olympiads, Free Geometry, Euclidean Geometry, Calculus, Geometric Construction. Oh yes, going-nowhere discussions, haikus, and poems too.
Showing posts with label Trapezoid. Show all posts
Showing posts with label Trapezoid. Show all posts
Monday, March 12, 2012
Friday, March 9, 2012
Fox 348
We'll return back to Sampy's question later. But, for a change let's see a simple one - or at least it looks simple. We're looking for the shortest proof of the claim below. May be purely-geometric one? Or is the claim wrong? Let us know...

Tuesday, February 23, 2010
Saturday, February 20, 2010
Fox 250
 http://www.8foxes.com/
http://www.8foxes.com/Bleaug submitted this one, saying that he got inspired by Yu's elegant solution to Fox 246. More is on the way...
Thursday, February 18, 2010
Fox 242 - Counterexample-2
Yu claims:
A rectangle is a trapezoid. The shaded area (2 equal triangles) = ¼ of the rectangle.
 The above trapezoid has the same area as the rectangle above. As P approaches Q, the height of the upper shaded triangle increases faster than the height of the lower shaded triangle decreases. .: the shaded area > ¼ of the trapezoid.
The above trapezoid has the same area as the rectangle above. As P approaches Q, the height of the upper shaded triangle increases faster than the height of the lower shaded triangle decreases. .: the shaded area > ¼ of the trapezoid.
A rectangle is a trapezoid. The shaded area (2 equal triangles) = ¼ of the rectangle.
 The above trapezoid has the same area as the rectangle above. As P approaches Q, the height of the upper shaded triangle increases faster than the height of the lower shaded triangle decreases. .: the shaded area > ¼ of the trapezoid.
The above trapezoid has the same area as the rectangle above. As P approaches Q, the height of the upper shaded triangle increases faster than the height of the lower shaded triangle decreases. .: the shaded area > ¼ of the trapezoid. Wednesday, February 10, 2010
Fox 242 - Counterexample
Bleaug has submitted this counterexample. He smells right :)
Easiest way is to get a counter-example:
assume the upper side of the trapezoid collapses to a single point,
the pink area corresponds to 1/4 of the trapezoid/triangle area.
The (non-empty) blue area is in excess.
Easiest way is to get a counter-example:
assume the upper side of the trapezoid collapses to a single point,
the pink area corresponds to 1/4 of the trapezoid/triangle area.
The (non-empty) blue area is in excess.
Sunday, February 7, 2010
Fox 242
Labels:
areas,
draw lines in the sand,
proof,
similarity of triangles,
Trapezoid
Saturday, February 6, 2010
Friday, February 5, 2010
Fox 241
YES, the solution has NOW been confirmed!!
We will post these excellent solutions here later!
There are at least one more slick solution, not identified yet!
Thank you guys for the great work!
Labels:
Gravity,
Isosceles Triangle,
Physics,
Statics,
Trapezoid,
Trigonometry
Tuesday, February 2, 2010
Fox 239
Make things as simple as possible, but not simpler.
Labels:
equilateral triangle,
heights,
Parallel Lines,
Trapezoid
Friday, January 29, 2010
Wednesday, January 27, 2010
Fox 236
There should be several purely geometric solutions.
Friday, January 15, 2010
Wednesday, January 13, 2010
Fox 226
Tuesday, December 22, 2009
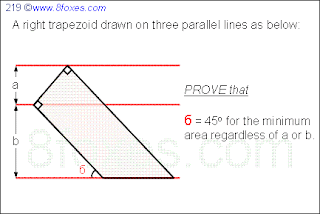
Fox 219
Friday, November 27, 2009
Thursday, October 29, 2009
Wednesday, October 28, 2009
Fox 169
Saturday, October 17, 2009
Fox 153
Think simple.
Math has nothing to do with numbers.
Try to see the connections.
http://www.8foxes.com/Home/153

Math has nothing to do with numbers.
Try to see the connections.
http://www.8foxes.com/Home/153

Subscribe to:
Posts (Atom)