Fox 357

Long time no see!!!

HELLO WORLD!!!

Hope everybody is doing alright.

Yeah, sure love each other, especially those who really need to be loved!

Let me now take another long break :)

Fox 333

http://www.8foxes.com/

Red Fox: Happy Pi+1 Day!
Himalayan Fox: What is that exactly?
Red: Well, March 14 was the Pi Day, you know, 3.14, and today is March 15th.
Himalayan: But Pi+1 would be 4.14 which is April 14th, isn't it?
Red: Oh, I didn't think that way. Whatever it is, happy March 15th to you brother.
Himalayan: OK, I'll mechanically say "to you too", but can we really happy while thousands of souls swept away with the water?
Red: Well, we can not die with the dead.
Himalayan: But we can help the living.
Red: I hear you brother.
Himalayan: Then we can celebrate 2Pi Day a few months later.

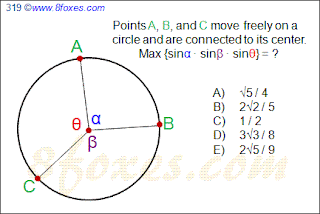
Fox 319 - Solutions

Below are 2 distinct solutions for Fox 319...

A solution based on symmetry by Bleaug:


Trigonometry and calculus by Six:

x + y + z = 360 and sinx*siny*sinz

-> f(x,y) = sin(x)*sin(y)*sin(360-x-y)
-> f(x,y) = sin(x)*sin(y)*-sin(x+y)

Now to find the critical points of f(x,y), we just need to find the partial derivative with respect to x and y and solve for 0.

f_x(x,y) =

sin(x)sin(y)(-cos(x+y)-cos(x)sin(y)sin(x+y)

solve for 0.

sin(x)sin(y)(-cos(x+y)-cos(x)sin(y)sin(x+y)=0

-> tan(x) = -tan(x+y)

Since the function is symmetric, we should get the same partial derivative for y.

-> tan(y) = -tan(y+x)

-> tan(x)=tan(y)

-> x = y or they are opposites. However, if they are opposites, the original function just becomes 0. Thus, x = y.

Now substitute in x for y in the original equation and find its critical points.

Eventually, you will get sin(3x)=0

x = 120 degrees
y = 120 degrees
z = 120 degrees

Answer (D)

http://www.8foxes.com/

Fox 319

http://www.8foxes.com/

Fox 315

http://www.8foxes.com/

Polar Fox: I have a problem with this one!

Red Fox: What's wrong with it?

Polar Fox: Nothing moves continuously?

Red Fox: Come again?!

Polar Fox: The universe is discrete! THERE IS NO CONTINUUM.

Red Fox: Then how do the things move, flow, or slide?

Polar Fox: Nothing moves! Absolutely nothing moves!!

Red Fox: But the time ticks away, no? Clock arms DO advance.

Polar Fox: No, they don't! But they die in one instance and resurrect in the next one. In between no measurable time passes. Matter oscillates between existence and non-existence continuously.

Red Fox: Continuously? Isn't that ironic?

Polar Fox: Between any two existence, there is nothing but emptiness.

Red Fox: I am having the feeling that your intelligence fall into non-existing state just now.

Polar Fox: Hold on. I think I am about to jump back into the reality. Wait a sec.

Red Fox: Take your time dude. Just take your time!

Fox 312 - Solutions

Two solutions for Fox 312 are identified below.

Bleaug:
As in Fox 262 (see its solution here) A area (= OQR area below) extremal/constant implies P midpoint of QR. Because:
A constant <=> dA = 0 <=> area(PRR') = area(PQQ') <=> area(P'RR') = area(P'QQ') => PR = PQ when dP tends towards 0.

Hence A = 1 = 2xy or y = 1/2x i.e. answer (D).

Migue:
If area is A the answer is f(x)=y=A/2x.
f(x) is the envelope of all straight lines that close in with axes X-Y constant area equals to A.
Equation of one of this lines is: x/a + y/b = 1 (a,0) in X & (0,b) in Y.
Notice that a & b are two variable parameters.Another equation is: ab/2 = A (area of triangle that straight line draws with axes).
(1) Let f(x,y,a,b)= bx+ay-ab = 0
(2) Let g(a,b)=ab-2A = 0
(3) f'a · g'b - f'b · g'a = 0 (Jacobian of derivatives respect to a and b parameters).

f'a is the derivative of f respect a, ...

y/b - x/a = 0 (3)

If we resolve this system of equations (1),(2) & (3) we obtain:
a = 2x & b = 2y -> ab = 4xy = 2A -> xy = A/2 (equilateral hyperbola)
and y = f(x) = A/2x.

Answer is D) for A =1.