Key words: Geometry, Unusual geometry, Math, Physics, Chemistry, High school, Geometry Olympiads, Free Geometry, Euclidean Geometry, Calculus, Geometric Construction. Oh yes, going-nowhere discussions, haikus, and poems too.
Saturday, March 26, 2011
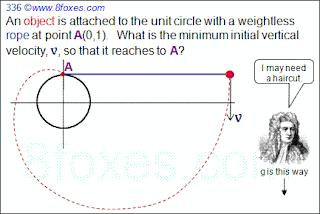
Fox 336
Friday, April 16, 2010
Fox 272 - Solution

Without the parabolic track a particle (initially at rest) at the vertex will be in free fall and drops at maximum acceleration of g. With the parabolic track the motion is restricted by the track and the particle is no longer in free fall; it slides down the track with increasing speed. Will it leave the track at some point?
All parabolic tracks are similar (See Fox 270). Consider the track y=-x^2 which ends at the point (x,-x^2).

When a particle slides from rest at the vertex (0,0) to the point (x,-x^2), it acquires speed v=sqrt(2gx) in the direction given by tanθ=dy/dx=-2x, where θ is the angle with the x-axis.
.: cosθ = 1/sqrt(1+4x^2), sinθ=-2/sqrt(1+4x^2).
At point (x,-x^2) the particle is in free fall,
v_H=sqrt(2gx)/sqrt(1+4x^2),
v_y=-2sqrt(2gx^2)/sqrt(1+4x^2).
After a further time Δt, Δx=sqrt(2gx)Δt/sqrt(1+4x^2),
Δy=-2sqrt(2gx^2)Δt/sqrt(1+4x^2) - (1/2)g(Δt)^2
= -2xΔx-(1+(1/4x^2))(Δx)^2,
and the particle is at y=-x^2 - 2xΔx -(1+(1/4x^2))(Δx)^2.
If the track did not end at (x,-x^2) but continued to infinity,
y=-(x+Δx)^2
= -x^2-2xΔx-(Δx)^2 > -x^2 - 2xΔx -(1+(1/4x^2))(Δx)^2.
.: The particle stays on the parabolic track.
Monday, April 5, 2010
Fox 272
Himalayan fox: Here is a claim ready to be blown away with a single counterexample. How strong is your theory Polar?
Polar fox: Well, I can smell it.
Himalayan fox: It demands more than that. Are you living in a paper castle ready to be drifted away by the next wind? Or are you a real believer of something that even the strongest quake can not shake you a bit - you stand firmly on the ground?
Polar fox: No problem on my stand man! I am not shaken at all, but... the thing is... the ice is melting!
Sunday, February 28, 2010
Fox 253 Solution