by Bleaug
Let's take as a parabola "well known" property that for any two points U, V of abscissa u, v, the tangent to point T of abscissa (u+v)/2 is parallel to vector UV. (OK! this demonstration would need some cartesian algebra but simple, promise!) From this we derive that for any point M between U and V the area of triangle UMV et less or equal to area of triangle ATV which maximizes triangle height (e.g. assume the opposite and compare area of triangle obtained from M+dM)

Then let's assume U and V achieve the maximum trapezoid area between A (x=0) and B(x=2), then necessarily Au=uv and uv=vB which implies Au=uv=vB=AB/3=2/3. Because of symmetry, maximum area is equivalent to area of rectangle AvVW = 8/9 * 4/3 = 32/27.
Geometric Translation
by Yu
Translate y=2x-x^2 to the left by 1 unit to obtain y=1-x^2.
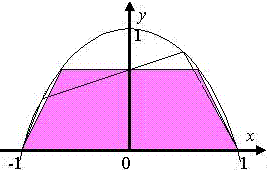
Without going into details, the area of the trapezium is greater than the area of the quadrilateral. Area of trapezium, A = (1/2) (2x+2)(1-x^2) = (x+1)(1-x^2)
Max A = 32/27 when x = 1/3.
For more details see Fox 260.
http://www.8foxes.com/

Yu:
ReplyDeleteYour translation makes the problem one notch easier. But by saying "Without going into details, the area of the trapezium is greater than the area of the quadrilateral.", you are skipping an important part. Although you answer is correct, that detail is not very intuitive. Your statement can be proven algebraically.
Find the iintersections of the line y=mx+c and the parabola. Work out the areas of the quadrilateral and the trapezium, then compare the areas. Yu
ReplyDeleteDo not use all of these Private Money Lender here.They are located in Nigeria, Ghana Turkey, France and Israel.My name is Mrs.Ramirez Cecilia, I am from Philippines. Have you been looking for a loan?Do you need an urgent personal or business loan?contact Fast Legitimate Loan Approval he help me with a loan of $78.000 some days ago after been scammed of $19,000 from a woman claiming to be a loan lender from Nigeria but i thank God today that i got my loan worth $78.000.Feel free to contact the company for a genuine financial call/whats-App Contact Number +918929509036 Email:(fastloanoffer34@gmail.com)
ReplyDelete