Fox 253 Solution

http://www.8foxes.com/

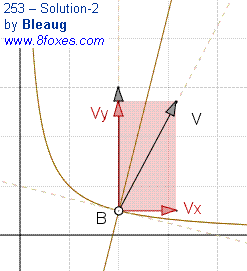
Bleaug goes on:

Energy acquired in free fall from rest position is 1/2.mV2=mg(h0-1/2)

Vertical velocity after bounce is V reduced by a factor equal to cos(2a), where a is the angle of tangent to 1/x at B: Vy = V.cos(2a) and tan(a)=-1/4

Highest point reached after bounce is such that: 1/2.mVy2=mg(h-1/2), so h = 1/2 + cos(2a)2.(h0-1/2)

From simple trigonometry we get cos(2a) = 1-tan(a)2/(1+tan(a)2) = 15/17

So h = 1/2 + (15/17)2 . (h0-1/2) = 1/2 + (225/289). 289/2 = 113.

Fox 255

http://www.8foxes.com/
Shelby suggested this problem. Thanks!

Fox 251 Solution-1

http://www.8foxes.com/

Here is Fox 251.

Fox 254

http://www.8foxes.com/

This is just a model for a very basic structure in Organic Chemistry. Real molecules are more dynamic than this. Atoms vibrate even at very low temperatures.

Fox 252 - Solution-2

http://www.8foxes.com/

See Fox 252

Fox 252 - Solution-1

http://www.8foxes.com/
See Fox 252

Fox 253

http://www.8foxes.com/

The answer is now confirmed! Will post later...

Fox 251

http://www.8foxes.com/

Fox 236 - Solution-1

See the original problem: Fox 236

http://www.8foxes.com/

Let simplicity ring all accross the land...

Fox 252

http://www.8foxes.com/

All along the wall, between us

I see a teacher, there for us

I look at the wall, I see right through it

I lean on the wall, there for us

Fox 248 - Solution-2

http://www.8foxes.com/

Bleaug states:
Let's take a, b, c to be the sides of A, B, C squares
By construction, the sum of the two shorter sides of D is equal to c. Same result for E.
All right triangles in the picture are similar, so are D and E.
Similar triangles with equal lengths implies D and E are identical (assertion 2)
The two shorter sides of D and E are a and b. So a+b=c (assertion 1)
Triangle D is to F as G is to E, as b is to a. So F/D=E/G=(b/a)^2. Since E=D we get F.G=E^2=D^2 (assertion 3)

Fox 248 - Solution-1

http://www.8foxes.com/

Fox 250

http://www.8foxes.com/
Bleaug submitted this one, saying that he got inspired by Yu's elegant solution to Fox 246. More is on the way...

Fox 249

http://www.8foxes.com/

Fox 242 - Counterexample-2

Yu claims:
A rectangle is a trapezoid. The shaded area (2 equal triangles) = ¼ of the rectangle.


The above trapezoid has the same area as the rectangle above. As P approaches Q, the height of the upper shaded triangle increases faster than the height of the lower shaded triangle decreases. .: the shaded area > ¼ of the trapezoid.

Fox 248

http://www.8foxes.com/

Never delay a good idea.

Once you let it go,

it may never have a chance to resurrect.

--- Himalayan Fox

Fox 247

http://www.8foxes.com/

Fox 246

http://www.8foxes.com/

Fox 245

http://www.8foxes.com/
Ignore the curvatures, SpongeBob gets wobbly when he's overjoyed.
By the way, SpongeBob and Patrick are owned by Viacom International, Inc.
Freedom to the Bikini-Bottom!

Fox 243 - Solution

http://www.8foxes.com/

Bleaug claims the following:

Almost a pure geometric proof this time (only requires Pythagorean theorem).

- TIJ is the section of the pyramid by a plane orthogonal to base and parallel to BC and AD

- by construction, TI is orthogonal to AB, and TJ to CD

- hence: AT^2-BT^2 = AI^2+IT^2-BI^2-IT^2 = AI^2-BI^2, similarly DT^2-CT^2 = DJ^2-CJ^2

- since AIB is a translation of DJC: AT^2-BT^2 = DT^2-CT^2

- from which we get DT^2 = AT^2-BT^2+CT^2 = 9-2+1 = 8

Fox 244

http://www.8foxes.com/

Look into thy heart, and see,

it desireth to fly in Heavens,

whilst there are knots pulling thee

to cruelly darketh corners!
--- Dervish Fox

Fox 242 - Counterexample

http://www.8foxes.com/

Bleaug has submitted this counterexample. He smells right :)

Easiest way is to get a counter-example:
assume the upper side of the trapezoid collapses to a single point,
the pink area corresponds to 1/4 of the trapezoid/triangle area.
The (non-empty) blue area is in excess.

Fox 243

http://www.8foxes.com/

Answer not confirmed again.

Fox 242

http://www.8foxes.com/

A nice counterexample was found!

Fox 221 - Solution - 2

http://www.8foxes.com/

Fox 221 - Solution - 1

http://www.8foxes.com/

Fox 241

YES, the solution has NOW been confirmed!!

We will post these excellent solutions here later!

There are at least one more slick solution, not identified yet!

Thank you guys for the great work!

http://www.8foxes.com/

Fox 240

http://www.8foxes.com/

Now this asks little more than geometry.

Note that the random process described in the question is discrete.

Ladybugs "appear" in next vertices at the same time.

Fox 239

http://www.8foxes.com/

Make things as simple as possible, but not simpler.

Fox 238

http://www.8foxes.com/

Another classic!